7th January 1610 was the day Galileo Galilei, with his self-made telescope, became the first person to observe the moons of Jupiter; just a day later, on 8 January, Simon Marius had also independently observed these moons. The names we use today for the four moons, namely, Io, Europa, Ganymede and Callisto, were given by Simon Marius. Galileo made significant conclusions from his observations; he concluded that these moons orbited Jupiter and found their time period. This was a remarkable result as it gave solid evidence for the heliocentric model of the solar system. So we set out to rediscover Galileo's results on the orbital periods of Jupiter's moons.
Our experiment aimed to find the orbital period of the moons of Jupiter using a CMOS sensor and an 8-inch reflective telescope. We proceeded to the experiment by performing a simulation in the Stellarium software; from this, we could sketch out the procedure for our experiment. The first part of the experiment was to collect data, and this was done by taking pictures of Jupiter and its moons every day at around the same time for 15 days (10-11-2022 to 25-11-2022) by the students in NAC. Then, we had to filter our data and select the best images. We had to make our images speak to us, and by speaking we mean that we had to translate the observational data to something we could work with and do further analysis. To accomplish this, we ran our images in a code that was written by R Vasanth Kashyap(B19), and this code returned us the pixel coordinate of Jupiter and its moons. By using the pixel coordinates, we found the cartesian distance between Jupiter and its moons.

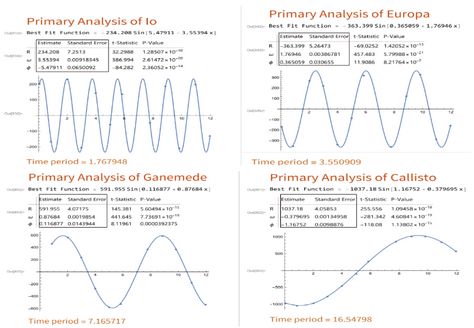
The second part of the experiment was to analyze this data. we didn’t know which point corresponds to which moon, so we began our analysis by assuming that the moons follow a circular orbit; we have enough observation such that the radius of the moon has been observed for all moons, the radius and time-period of each moon is very different and, the time-period of any moon is not less than 1 Earth day. We made a table with distances of all moons w.r.t Jupiter w.r.t. time. From this table, we selected the maximum distance. We divided all the distances by this number, we then took the sin inverse of all these ratios, and we plotted these points w.r.t. to time and did a straight fit to identify which points are following a sinusoidal pattern, after selecting these points we then removed these points from the table and repeated the whole process again(but now the maximum distance would have changed to be explicit reduced), we did this for four times. We then used these selected points and put them in a code that fit them to sin curves and gave us the angular frequencies, and from this, we calculated the time periods of different moons. After finding the time period, we could identify Io, Europa, Ganymede and Callisto. The orbital periods we obtained were,
- For Io = 1.768 ± 0.009 earth days
- For Europa = 3.551 ± 0.004 Earth days
- For Ganymede = 7.166 ± 0.002 Earth days
- For Callisto = 16.548 ± 0.001 Earth days
We can see that the errors associated with their values are very low; this was the advantage we got from using the CMOS sensor. The maximum absolute percentage error w.r.t. the accepted values of the orbital periods was 0.85% which was less than a percent!
We further extended our experiment to find the mass of Jupiter, and we proceeded to do this by first calculating how much distance 1 pixel corresponds to using the size of Jupiter from the literature. We then used this to find the radius of the orbit of the moons, which was in pixels that had been obtained from the sin curve fitting and their corresponding orbital periods, to calculate the actual mass of Jupiter. The mass of Jupiter we found was ( 1.737 ± 0.004 ) ⨯ 10^27 Kg, which again was remarkably close to the accepted value, i.e. ( 1.8981 ± 0.0002 ) ⨯ 10^27 Kg. We thank everyone who was part of this experiment. And this concludes our experiment.